
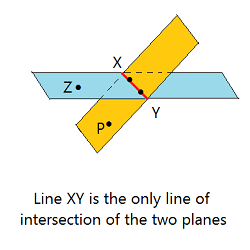
- #Line point postulate definition geometry series#
- #Line point postulate definition geometry download#
Question 3: What are the uses of Euclidean geometry?Īnswer: We use Euclidean geometry to design buildings, predict the location of moving objects, and survey land. Lastly, if the straight-line intersect two other straight-lines, and make the two interior angles on one side of it together less than two right angles, then the other straight line will meet at a point on the side with less than two right angles.It can be described as a circle with any given point as its center and any distance as its radius.You can extend a straight-line to a finite length.You can draw a straight-line segment from any given point to others.Question 2: State the five postulates of Euclidean geometry?Īnswer: Five common postulates of Euclidean geometry are: In the figure below, as you can see that as α + β < 180, the two lines when produced meet the side on which the sum of angles is less than two right angles (shown here by dots). If a straight line falling on two straight lines makes the interior angles on the same side of it, taken together = less than two right angles (All right angles are equal to one another.A circle may be described with any radius and any centre.
#Line point postulate definition geometry download#
You can download Introduction to Euclid’s Geometry Cheat Sheet by clicking on the download button below As you can see in the above image, line 1 and line 2 are parallel if and only if the sum of angles ‘a’ and ‘b’ they make with the transversal is 180 degrees. ‘Parallel lines’ are a set of 2 or more lines that never cross or intersect each other at any point in space if they are extended indefinitely.

Two lines are parallel to each other if they intersect the third line and the interior angle between them is 180 degrees. So, irrespective of the length of a right angle or its orientation all right angles are identical in form and coincide exactly when placed one on top of the other. A right angle is an angle measuring 90 degrees. Postulate – IVĪll right angles are congruent or equal to one another. In the above example, the line segment AO serves as the radius of a circle with centre at point O and a diameter equal to AB where l(AB) =2 l(AO). If one of these points is taken as the centre of a circle and the radius of the circle is taken as equal to the length of the segment, a circle can be drawn with its diameter twice than the length of the line segment. Consider a line segment bounded by two points. For any line segment, a circle can be drawn with its centre at one endpoint and the radius of the circle as the length of the line segment. A line is uniquely defined as passing through two points which are used to name it.Ī circle can be drawn with any centre and any radius.

Unlike a line segment, a line is not bounded by any endpoint and so can be extended indefinitely in either direction.

Postulate – IIĪny straight line can be extended indefinitely on both sides. A line segment is named after the two endpoints with an overbar on them. Thus a line segment is measurable as the distance between the two endpoints.
#Line point postulate definition geometry series#
It consists of a series of points bounded by the two endpoints. In Geometry, a line segment is a part of a line that is bounded by 2 distinct points on either end. Postulate – IĪ straight line segment can be formed by joining any two points in space. We will see a brief overview of some of them here. There are 23 definitions or Postulates in Book 1 of Elements (Euclid Geometry). Euclid introduced the fundamentals of geometry in his book called “Elements”. He is credited with profound work in the fields of algebra, geometry, science, and philosophy. ‘Euclid’ was a Greek mathematician regarded as the ‘Father of Modern Geometry‘. The postulates stated by Euclid are the foundation of Geometry and are rather simple observations in nature. Any statement that is assumed to be true on the basis of reasoning or discussion is a postulate or axiom.


 0 kommentar(er)
0 kommentar(er)
